Deep learning and optimal control: what’s the connection?
Optimal control → more stable and accurate deep learning One famous interpretation of ResNet(Residual network) is to view the layer-to-layer transformation Deep learning → more efficient optimal control solvers On the other hand, physics informed neural networks(PINN) offers an approach to solve high dimensional PDEs without a computational grid. Some control problems need to solve a high dimensional Hamilton-Jacobi-Bellman equation, which may take advantage of this.
For example, the following figure is a slice of a 4D distance function trained with data generated from Eikonal solutions with black dots as sources. This slice shows the shortest distance from each point in a domain(with an obstacle) towards the source (0.3,0.1). 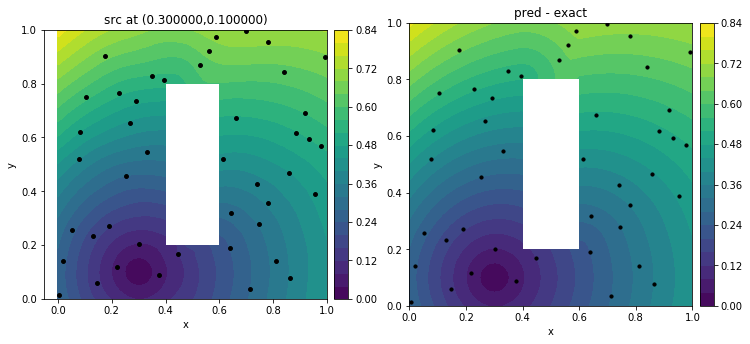
$$u_{n+1} = u_n + h \sigma (W_n u_n + b_n)$$
For example, the following figure is a slice of a 4D distance function trained with data generated from Eikonal solutions with black dots as sources. This slice shows the shortest distance from each point in a domain(with an obstacle) towards the source (0.3,0.1).

